
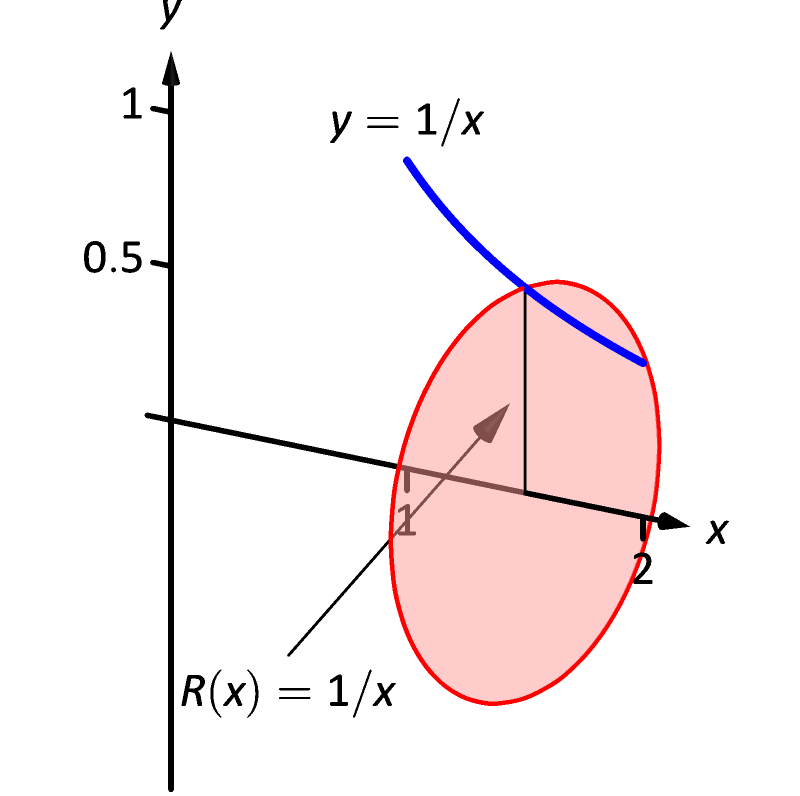
With the shift to the right, think of it as adding on the little bit at the beginning ( x=0 to x=1) that Sal didn't include as part of his problem but removing the (larger) bit at the other end (x=3 to x=4.) The shape moved but the boundaries of integration didn't so you're integrating a different part of the overall shape. Unless I'm drunk, with just the shift up 1, rotating around y=1 should get you the same answer as rotating the un-shifted function around y=0 so the reasoning from before still stands. We already went over going up 1 in the first answer. Of course, 4 ≠ 5.Ģ: You shifted the whole function up 1 and to the right 1. The radius if the function is rotated around the x-axis is 5 (5-0). So the radius when it's rotated around y=1 will be 4 (5-1) making the diameter 8. The function y=√(x) will have a y value of 5. I assume by "regular disc," you mean one that has been rotated around y=0 (the x-axis.) The diameter of the disc whose "circle part" is centered on y=1 is only the same as the radius of a disc centered on y=0 at x=4 (in this example.) Think about moving to a different spot along the function. To put simply though, the bit of the function that Sal integrated and the 2 that you did in your 2 questions are 3 different shapes.ġ: Perhaps it seems that way because of the place he chose to draw his disc. These are much more difficult to answer with words than pictures but I'll do my best. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. We recommend using aĪuthors: Gilbert Strang, Edwin “Jed” Herman Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format,
DISK GRAPH CALCULUS LICENSE
Want to cite, share, or modify this book? This book uses theĬreative Commons Attribution-NonCommercial-ShareAlike License Substituting these terms into the expression for volume, we see that when a plane region is rotated around the line x = − k, x = − k, the volume of a shell is given by Then, the outer radius of the shell is x i + k x i + k and the inner radius of the shell is x i − 1 + k. Suppose, for example, that we rotate the region around the line x = − k, x = − k, where k k is some positive constant. If, however, we rotate the region around a line other than the y -axis, y -axis, we have a different outer and inner radius. This was based on a shell with an outer radius of x i x i and an inner radius of x i − 1. V shell = f ( x i * ) ( π x i 2 − π x i − 1 2 ) = π f ( x i * ) ( x i 2 − x i − 1 2 ) = π f ( x i * ) ( x i + x i − 1 ) ( x i − x i − 1 ) = 2 π f ( x i * ) ( x i + x i − 1 2 ) ( x i − x i − 1 ).
Previously, regions defined in terms of functions of x x were revolved around the x -axis x -axis or a line parallel to it. Note that this is different from what we have done before. We then revolve this region around the y-axis, as shown in Figure 2.25(b).
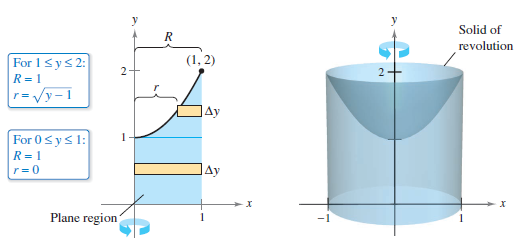
As before, we define a region R, R, bounded above by the graph of a function y = f ( x ), y = f ( x ), below by the x -axis, x -axis, and on the left and right by the lines x = a x = a and x = b, x = b, respectively, as shown in Figure 2.25(a). The Method of Cylindrical ShellsĪgain, we are working with a solid of revolution. In the last part of this section, we review all the methods for finding volume that we have studied and lay out some guidelines to help you determine which method to use in a given situation. Also, the specific geometry of the solid sometimes makes the method of using cylindrical shells more appealing than using the washer method.
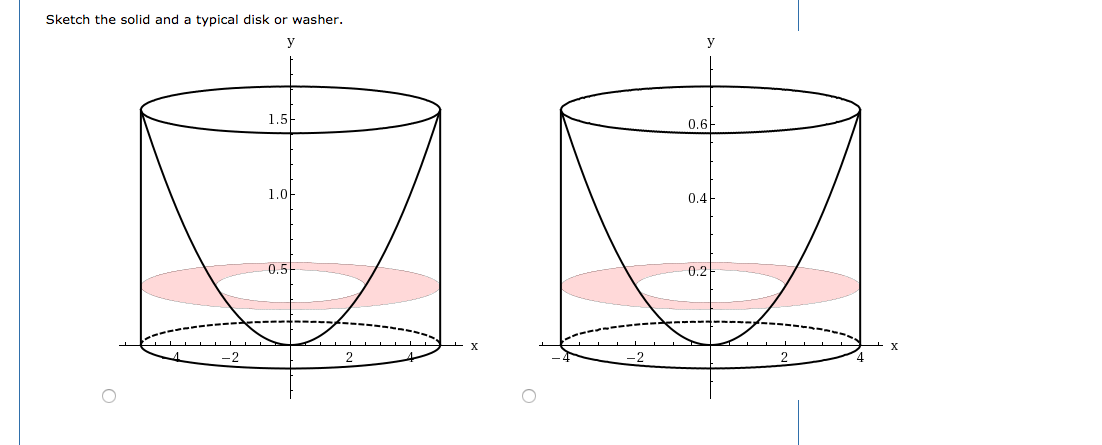
The ability to choose which variable of integration we want to use can be a significant advantage with more complicated functions. With the method of cylindrical shells, we integrate along the coordinate axis perpendicular to the axis of revolution. We can use this method on the same kinds of solids as the disk method or the washer method however, with the disk and washer methods, we integrate along the coordinate axis parallel to the axis of revolution. In this section, we examine the method of cylindrical shells, the final method for finding the volume of a solid of revolution. 2.3.2 Compare the different methods for calculating a volume of revolution.2.3.1 Calculate the volume of a solid of revolution by using the method of cylindrical shells.


 0 kommentar(er)
0 kommentar(er)
